Věta o střední hodnotě diferenciálního počtu

Kategorie: Nezařazeno (celkem: 23181 referátů a seminárek)

Informace o referátu:

Příbuzná témata

Vytisknout referátPřidat referát do záložek

Věta o střední hodnotě diferenciálního počtu

Tento článek pojednává o větě z matematické analýzy. Další významy jsou uvedeny v článku Lagrangeova věta.

Věta o střední hodnotě diferenciálního počtu (také Lagrangeova věta o střední hodnotě, Lagrangeova věta o přírůstku funkce) je matematická věta z oblasti diferenciálního počtu, která říká, že se při „hladké“ změně nějaké veličiny v nějakém okamžiku dosahuje průměrné rychlosti dané změny.

Obsah

Rolleova věta

Podrobnější informace naleznete v článku Rolleova věta.

Speciálním jednodušším případem Lagrangeovy věty je Rolleova věta, ze které již věta Lagrangeova snadno plyne:

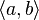Nechť funkce f(x) , je spojitá na intervalu langle a,b angle, má derivaci v každém bodě intervalu (a,b) , a platí f(a)=f(b) ,. Pak existuje bod c in (a,b) takový, že f^prime(c)=0.

Geometrický význam

Geometrické znázornění Rolleovy věty
Geometrické znázornění Rolleovy věty

Rolleova věta říká, že za uvedených předpokladů existuje v intervalu (a,b) , bod, v němž je tečna ke grafu funkce f(x) , rovnoběžná s osou x.

Fyzikální význam

Fyzikálně lze Rolleovu větu interpretovat takto:

Mění-li se nějaká veličina v čase „hladkým způsobem“ tak, že na začátku i konci tohoto procesu má stejnou velikost, pak v nějakém okamžiku musí být okamžitá rychlost změny nulová.

Lagrangeova věta o střední hodnotě

Lagrangeovu větu lze vyslovit následovně:

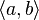Nechť funkce f(x) , je spojitá na intervalu langle a,b angle a má v každém bodě intervalu (a,b) , derivaci. Pak existuje bod c in (a,b) takový, že platí f^prime(c) = frac{f(b)-f(a)}{b-a}.

Geometrický význam

Geometrický význam Lagrangeovy věty
Geometrický význam Lagrangeovy věty

Lagrangeova věta tvrdí, že za uvedených předpokladů v intervalu (a,b) , existuje bod c ,, v němž je tečna k funkci f(x) , rovnoběžná s přímkou vedenou body (a,f(a)) , a (b,f(b)) ,.

Fyzikální význam

Lagrangeovu větu lze fyzikálně interpretovat následovně:

Mění-li se nějaká veličina v čase „hladkým způsobem“, pak v nějakém okamžiku musí být okamžitá rychlost změny rovna průměrné rychlosti.

Zobecnění

Zobecněním Lagrangeovy věty je Cauchyova věta o střední hodnotě:

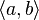Nechť funkce f(x), g(x) , jsou spojité na intervalu langle a,b angle, mají v každém bodě x , intervalu (a,b) , derivaci a nechť pro všechna x in (a,b) platí g^prime(x) eq 0. Pak existuje bod c in (a,b) takový, že platí frac{f^prime(c)}{g^prime(c)} = frac{f(b)-f(a)}{g(b)-g(a)}.

Důkaz

Dokážeme Cauchyovu větu o střední hodnotě, Lagrangeova věta pak plyne z Cauchyovy věty volbou g(x)=x ,. Protože g^prime(x) eq 0 pro všechna x in (a,b), je podle negace Rolleovy věty (důkaz) nutně g(a) eq g(b) (ostatní předpoklady Rolleovy věty jsou splněny díky předpokladům Cauchyovy věty). Můžeme tak definovat funkci

F(x)=-f(x)+frac{f(b)-f(a)}{g(b)-g(a)}(g(x)-g(a)).

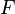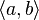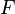Funkce F , je zřejmě spojitá na intervalu langle a,b angle, má derivaci na intervalu (a,b) , a F(a)=F(b)=-f(a) ,. F , splňuje předpoklady Rolleovy věty a existuje tedy c in (a,b) takové, že

0=F^prime(c)=-f^prime(c)+frac{f(b)-f(a)}{g(b)-g(a)}g^prime(c)

Dle předpokladu je g^prime(c) eq 0 a tedy

frac{f^prime(c)}{g^prime(c)}=frac{f(b)-f(a)}{g(b)-g(a)}.

Související články


Vytisknout referátPřidat referát do záložek

Nový příspěvek


Ochrana proti spamu. Kolik je 2x4?


Na-mobil.cz

Spřátelené weby

Přidat stránku k oblíbeným

Nejnovější v diskusi

Diskusní fórum »

TIP: Chcete zkrátit dlouho chvíli sobě nebo blízkému?
Klikněte na Puzzle-prodej.cz a vyberte si z 5000 motivů skladem!
TIP: Hračky a hry za dobré ceny?
Klikněte na Hračky obchod.cz a vyberte si z tisícovky hraček skladem!