Nula
Kategorie: Nezařazeno (celkem: 23181 referátů a seminárek)
Informace o referátu:
- Přidal/a: anonymous
- Datum přidání: 04. srpna 2008
- Zobrazeno: 2344×
- Licence: GNU Free Documentation License
- Seznam autorů a změn
- Vyloučení odpovědnosti
Příbuzná témata
Nula
Nula (z latiny nullus – žádný) je číslo 0, jedna z nejzákladnějších matematických konstant. Má tu vlastnost, že pro každé číslo a platí
- a + 0 = a
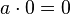
Číslo 0 na číselné ose odděluje záporná čísla od kladných. Nula je také číslice, která se používá v numerických systémech, kde pozice číslice je důležitá pro její skutečnou hodnotu. Na následující pozici má číslice vyšší hodnotu a číslice 0 se používá k posunu číslice na následující pozici. Např. v desítkové soustavě má číslice 1 v zápise 100 hodnotu sto. V teorii množin je nula velikost (kardinalita) prázdné množiny.
Obsah |
Číslo nula
Číslo nula má některé zvláštní vlastnosti, které je potřeba při provádění početních operací brát v úvahu.
Sčítání
Nula je z matematického hlediska při sčítání neutrální prvek. To znamená, že platí
- a + 0 = 0 + a = a
Násobení
Při provádění násobení platí
Říká se, že nula je absorbční prvek násobení.
Umocňování
Při umocňování platí
- a0 = 1.
I ve speciálním případě se někdy definuje
- 00 = 1, ve vyšší matematice však tento výraz není definován.
viz též nula na nultou.
Dělení nulou
- Podrobnější informace naleznete v článku Dělení nulou.
Výsledek dělení libovolného čísla nulou nelze jednoznačně zjistit. Proto je výsledek takové operace v matematice nedefinován.
Pro přirozená čísla můžeme operaci dělení nahradit opakovaným odečítáním. Pak můžeme hledat odpověď na otázku např. „Kolikrát musíme odečíst 4 od 12, abychom dostali výsledek 0?“ (kolik je 12 děleno 4?):
- 12 - 4 = 8
- 8 - 4 = 4
- 4 - 4 = 0
- Počet odečítání jsou 3.
- a tedy 12 : 4 = 3.
Pokud chceme vypočítat 12 : 0, pak otázka zní: „Kolikrát musíme odečíst 0 od 12, aby výsledek byl 0?“ Žádný počet operací však nevede k požadovanému výsledku.
