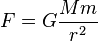Keplerovy zákony

Kategorie: Nezařazeno (celkem: 23181 referátů a seminárek)

Informace o referátu:

Příbuzná témata

Vytisknout referátPřidat referát do záložek

Keplerovy zákony

Keplerovy zákony jsou tři fyzikální zákony popisující pohyb planet kolem Slunce. Platí však obecněji pro pohyb libovolného tělesa v centrálním silovém poli, tedy v oblasti působení nějaké dostředivé síly, jejíž přitažlivost klesá s druhou mocninou vzdálenosti stejně jako gravitace výrazně hmotnějšího tělesa. Lze je tedy použít například i na pohyb Měsíce či umělé družice kolem Země, avšak s menší přesností, neboť vliv Slunce je v tomto případě nezanedbatelný.

Obsah

Historie

Johannes Kepler při odvození těchto zákonů využil systematická a ve své době nejpřesnější astronomická měření Tychona Brahe, jemuž byl Kepler asistentem v letech 1600 až 1601. První dva zákony vydal ve svém díle Astronomia nova (1609), třetí vyšel roku 1618 v Harmonices mundi. Později (1687) Isaac Newton ukázal, že Keplerovy zákony jsou důsledkem jeho obecnější fyzikální teorie mechaniky a gravitace.

Formulace zákonů

1. Keplerův zákon

Keplerův první zákon.
Keplerův první zákon.
Planety obíhají kolem Slunce po eliptických drahách, v jejichž jednom společném ohnisku je Slunce.

Význam 1. Keplerova zákona

Tento zákon popisuje tvar trajektorií planet pohybujících se v gravitačním poli Slunce.

Tento zákon říká, že planety se pohybují po rovinných křivkách (elipsách či kružnicích), kolem stálého středu (centra). To znamená, že vektor zrychlení, a tedy i síla způsobující tento pohyb leží v rovině dráhy. Planety se periodicky vzdalují a přibližují ke Slunci.

Planety obíhají kolem Slunce, takže geocentrický popis nebeské mechaniky již není vhodný.

Planety ale nemají příliš výstřednou dráhu (kromě plutoidu Pluta), takže v prvním přiblížení lze uvažovat, že se pohybují po kružnici. Tento zákon však platí i pro komety, které se pohybují po značně výstředných drahách. Pravděpodobnost, že by se nějaké těleso (dlouhodobě) pohybovalo okolo Slunce přesně po kružnici, je nulová, protože kružnice je ideální případ, ke kterému se lze v praxi pouze přiblížit ale nelze ho dosáhnout.


Roviny trajektorií všech planet procházejí středem Slunce. Slunce se nachází v ohnisku trajektorie každé planety. Hlavní vrchol elipsy, v němž je planeta nejblíže Slunci se nazývá přísluní (perihélium), hlavní vrchol, v němž je planeta nejdále od Slunce se nazývá odsluní (afélium).

2. Keplerův zákon

Plocha opsaná průvodičem planety za stejný čas.
Plocha opsaná průvodičem planety za stejný čas.
Keplerův druhý zákon.
Keplerův druhý zákon.
Obsahy ploch opsaných průvodičem planety (spojnice planety a Slunce) za stejný čas jsou stejně velké.

Průvodič planety je spojnice hmotného středu planety s hmotným středem Slunce. Velikost i směr průvodiče se při pohybu planety kolem Slunce neustále mění. Průvodič však vždy za stejnou dobu opíše plochu se stejným obsahem. To je důvodem, proč se tento zákon někdy nazývá zákon ploch.

Význam 2. Keplerova zákona

Planety se v přísluní pohybují nejrychleji, v odsluní zase nejpomaleji.

Ve výpočtech se používá plocha opsaná průvodičem za infinitezimálně (nekonečně) krátký čas, kdy se může zanedbat zakřivení trajektorie planety a celý výpočet se redukuje na vyjádření obsahu trojúhelníka. Druhý Keplerův zákon je jiné vyjádření zákona zachování momentu hybnosti. Plyne z něj, že oběžná rychlost planet se zmenšuje se vzrůstající vzdáleností od Slunce (těles od centrálního tělesa).

Plošná rychlost

Sledujeme-li pohyb tělesa s polohovým vektorem mathbf{r} v gravitačním poli, pak za čas dt dojde ke změně průvodiče na mathbf{r}+mathrm{d}mathbf{r}, kde elementární přírustek mathrm{d}mathbf{r} spadá do směru dráhy. Obsah elementární plochy opsané tímto průvodičem lze vyjádřit ve tvaru

mathrm{d}S = frac{1}{2}(mathbf{r} imesmathrm{d}mathbf{r})

Pro plošnou rychlost pak s pomocí tohoto vztahu získáme výraz

mathbf{w} = frac{mathrm{d}S}{mathrm{d}t} = frac{1}{2}(mathbf{r} imes frac{mathrm{d}mathbf{r}}{mathrm{d}t}) = frac{1}{2}(mathbf{r} imesmathbf{v})

Vektor plošné rychlosti 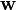mathbf{w} je kolmý k rovině, v níž leží trajektorie pohybu. Tento Keplerův zákon říká, že pro plošnou rychlost platí

mathbf{w}=mbox{konst}


Ze znalosti vztahu pro moment hybnosti 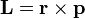mathbf{L}=mathbf{r} imesmathbf{p}, kde mathbf{p}=mmathbf{v} je hybnost planety, lze psát

mathbf{L}=2mmathbf{w}

Je-li tedy konstantní plošná rychlost, je konstantní také moment hybnosti. Obráceně lze říci, že ze zákona zachování momentu hybnosti vyplývá konstantní plošná rychlost pohybu planety v radiálním gravitačním poli (a tedy také druhý Keplerův zákon).

Plošné zrychlení

Derivací plošné rychlosti podle času dostaneme plošné zrychlení

mathbf{q} = frac{mathrm{d}mathbf{w}}{mathrm{d}t} = frac{1}{2}left(mathbf{r} imesfrac{mathrm{d}mathbf{v}}{mathrm{d}t} ight) + frac{1}{2}left(frac{mathrm{d}mathbf{r}}{mathrm{d}t} imesmathbf{v} ight) = frac{1}{2}left(mathbf{r} imesfrac{mathrm{d}mathbf{v}}{mathrm{d}t} ight) = frac{1}{2}(mathbf{r} imesmathbf{a}),

kde bylo využito toho, že frac{1}{2}left(frac{mathrm{d}mathbf{r}}{mathrm{d}t} imesmathbf{v} ight) = 0.

Při planetárním pohybu je plošná rychlost stálá a plošné zrychlení tedy musí být nulové. To znamená, že mathbf{r} imesmathbf{a}=0. Vektorový součin dvou vektorů je nulový, je-li jeden z nich nulový, nebo pokud leží v jedné přímce (tzn. mají shodný nebo přesně opačný směr). Avšak mathbf{r} ani mathbf{a} není nulové, neboť pohyb probíhá v určité vzdálenosti od středu (tedy mathbf{r} e 0) a při každém křivočarém pohybu se vyskytuje nějaké zrychlení (tedy mathbf{a} e 0). Znamená to tedy, že zrychlení mathbf{a} (tedy i odpovídající síla) leží ve směru průvodiče mathbf{r}.


Trajektorie dráhy má vždy takový tvar, že vzhledem k tečnému vektoru se vždy zakřivuje směrem k centru. To znamená, že zrychlení směřuje dovnitř uzavřené dráhy (elipsy). V opačném případě by se dráha zakřivovala ven od tečného vektoru a dráha by se neuzavřela. Důsledkem je, že vektor zrychlení směřuje vždy do centra silového působení. Takové silové působení se nazývá centrální. Také pohyb způsobený těmito silami se nazývá centrální pohyb.

3. Keplerův zákon

Poměr druhých mocnin oběžných dob dvou planet je stejný jako poměr třetích mocnin jejich velkých poloos (středních vzdáleností těchto planet od Slunce).

Pokud označíme T1 a T2 oběžné doby dvou planet a a1 a a2 délky jejich hlavních poloos, pak lze tento zákon vyjádřit ve tvaru

frac{T_1^2}{T_2^2} = frac{a_1^3}{a_2^3}

Tento zákon platí v tomto tvaru jen tehdy, jsou-li hmotnosti planet zanedbatelně malé ve srovnání s hmotností Slunce, což je u planet Sluneční soustavy splněno.

Význam 3. Keplerova zákona

Planety blízko Slunce jej oběhnou za kratší čas než planety vzdálené.

Odvození

Předpokládejme, že soustava spojená se Sluncem je inerciální. Excentricity drah planet jsou malé, takže je můžeme považovat za přibližně kruhové. Bližší planety mají větší oběžnou rychlost, protože na ně Slunce působí větší silou. Oběžná rychlost jde vyjádřit z gravitační síly, která je zde silou dostředivou:

F_{ m g}=F_{ m o} quadLongrightarrowquad G frac{M_{ m Sl.}cdot M_{ m pl.}}{R^2}= frac{M_{ m pl.}cdot v^2}{R} quadLongrightarrowquad v^2 = G frac{M_{ m Sl.}}{R} = frac{r_g}{2 R} c^2

kde

r_g = frac{2 G M_{Sl.}}{c^2}

je Schwarzschildův poloměr. Vidíme tedy, že čím je planeta blíže Slunci, tím rychleji obíhá kolem něho. Protože

v cdot T = s = 2 pi R,

dostaneme dosazením

T^2 = frac{4 pi^2 R^3}{G M_{ m Sl.}} = (frac{8 pi^2}{r_g c^2})R^3,

což je vyjádření 3. Keplerova zákona.

Odvození Newtonova gravitačního zákona z Keplerových zákonů

Při planetárním pohybu je plošná rychlost stálá, jak plyne z druhého Keplerova zákona. Z konstantnosti plošné rychlosti vyplývá, že plošné zrychlení je nulové. Plošné zrychlení lze zapsat ve tvaru mathbf{q}= frac{mathrm{d}mathbf{w}}{mathrm{d}t}=frac{1}{2}(mathbf{r} imesmathbf{a}). Má-li tato hodnota být nulová, musí být nulový vektorový součin mathbf{r} imesmathbf{a}. Toho lze dosáhnout pouze tehdy, pokud je jeden z vektorů nulový, nebo pokud mají oba vektory stejný nebo opačný směr.

Poněvadž při křivočarém pohybu je zrychlení nenulové a polohový vektor je také nenulový, přichází do úvahy pouze druhá možnost, tzn. zrychlení i průvodič leží na jedné přímce. Znamená to tedy, že pole bodového zdroje je centrálním polem a tedy, že hledaná gravitační síla je funkcí vzdálenosti od tohoto centra, ale nezávisí např. na [[zeměpisná šířka|zeměpisné šířce].

Pro odvození velikosti radiálního zrychlení můžeme předpokládat, že těleso se kolem centra sil pohybuje po kružnici. Při rovnoměrném kruhovém pohybu, který pozorujeme v důsledku konstantnosti plošné rychlosti, se centrum nachází ve středu křivosti dráhy. Radiální zrychlení je tedy totožné s dostředivým zrychlením a má velikost

a = frac{v^2}{r} = romega^2 = frac{4pi^2}{T^2}r,

kde T je oběžná doba.

Podle třetího Keplerova zákona platí T2 = Cr3, kde C je konstanta. Zrychlení lze pak zapsat ve tvaru

a = frac{4pi^2r}{Cr^3} = kfrac{1}{r^2},

kde k je konstanta platná pro všechny planety.

Síla, kterou působí Slunce na planetu, má velikost

F = ma = kfrac{m}{r^2},

kde m je hmotnost planety. Planeta však zároveň podle třetího Newtonova zákona působí na Slunce stejně velkou silou F^prime = k^prime frac{M}{r^2}, kde M je hmotnost Slunce. Z rovnosti |F|=|F^prime| dostaneme km=k^prime M. Položíme-li G = frac{k}{M}=frac{k^prime}{m}=mbox{konst}, dostáváme Newtonův gravitační zákon ve známém tvaru

F = G frac{Mm}{r^2}

Související články

Vytisknout referátPřidat referát do záložek

Nový příspěvek


Ochrana proti spamu. Kolik je 2x4?


Na-mobil.cz

Spřátelené weby

Přidat stránku k oblíbeným

Nejnovější v diskusi

Diskusní fórum »

TIP: Chcete zkrátit dlouho chvíli sobě nebo blízkému?
Klikněte na Puzzle-prodej.cz a vyberte si z 5000 motivů skladem!
TIP: Hračky a hry za dobré ceny?
Klikněte na Hračky obchod.cz a vyberte si z tisícovky hraček skladem!