Rychlá navigace: obsah, klávesové zkratky, navigace, vyhledávání.

Vložit nový referát | Diskusní fórum

Entropie

Kategorie: Nezařazeno (celkem: 23181 referátů a seminárek)

Informace o referátu:

Přidal/a: anonymous
Datum přidání: 20. srpna 2008
Zobrazeno: 4807×
Licence: GNU Free Documentation License
Seznam autorů a změn
Vyloučení odpovědnosti

Příbuzná témata

Vytisknout referát Přidat referát do záložek

Entropie

Entropie je obecně veličina udávající míru neuspořádanosti zkoumaného systému nebo také míru neurčitosti daného procesu.

Termodynamická entropie

Termodynamický systém s nízkou entropií - nízkou neuspořádaností, a tedy vysokou schopností konat práci.

Termodynamický systém s vysokou entropií - vysokou neuspořádaností, a tedy nízkou schopností konat práci.

Termodynamická entropie, nebo v kontextu termodynamiky jen krátce entropie, představuje míru neuspořádanosti systému (např. molekul plynu).

Historie

Název entropie definoval Ludwig Boltzmann v roce 1887 a entropie se tak stala jedním ze základních konceptů nového oboru statistické fyziky.

Jiný přístup k entropii nabídl dříve Rudolf Clausius v kontextu klasické termodynamiky. Podle něj je entropie měřítkem „kvality“ tepla. Například teplo získané z horkého tělesa (například páry v parním stroji) může vykonat více užitečné práce než teplo získané z méně teplého tělesa (například ochlazováním kostky ledu). Entropie v tomto pojetí vyjadřuje vztah mezi množstvím přestupujícího tepla a teplotou.

Značení

Značka: S
Základní jednotka: joule na kelvin, značka J K^-1'

Jednotka entropie je zároveň jednotkou tepelné kapacity.

Výpočet

Entropii lze vyjádřit pomocí tepla $Q$ a teploty $T$ v diferenciálním tvaru jako

$mathrm{d}S = frac{delta Q}{T}$

Podíl tepla $Q$ a teploty $T$ bývá také označován jako redukované teplo. Při Carnotově cyklu je součet redukovaných tepel roven nule. Vzhledem k tomu, že libovolný vratný cyklus je možné aproximovat elementárními Carnotovými cykly, jejichž redukované teplo lze vyjádřit jako 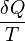$frac{delta Q}{T}$ , je možné předchozí tvrzení zobecnit na libovolný vratný cyklus.

Proběhnutí všech elementárních Carnotových cyklů je pak ekvivalentní aproximovanému vratnému ději, což lze vyjádřit jako

$sum frac{delta Q}{T} = 0$

Postupným zmenšováním elementárních Carnotových cyklů se v limitě dostaneme k výrazu

$oint frac{delta Q}{T} = 0$

Tento vztah je označován jako Clausiova rovnice a představuje podmínku, která je platná pro libovolný vratný kruhový děj. Tuto rovnici lze považovat za matematické vyjádření druhé hlavní věty termodynamiky.

Z předchozího vztahu je vidět, že všechna $? Q$ nemohou být kladná, ale některá musí být i záporná. Soustava, která vykonává vratný kruhový děj tedy nemůže od okolních těles teplo pouze přijímat, ale musí jim také nějaké teplo odevzdávat.

Princip růstu entropie

Entropie je veličina s velkým významem, neboť umožňuje formulovat druhou hlavní větu termodynamiky, a vyjádřit kvantitativně nevratnost tepelných pochodů. Tuto skutečnost vyjadřuje princip růstu entropie.

Jako příklad nevratného děje můžeme uvažovat zvednuté závaží s jistou potenciální energií. Pokud klesne závaží o určitou výšku $h$ a je zastaveno třením, vykoná práci $? W$ , při které třením vznikne teplo $? Q = ? W$ . Toto teplo odvedeme do okolí, které lze považovat za těleso s teplotou $T$ , a jehož entropie se tím změní o hodnotu 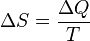$Delta S=frac{Delta Q}{T}$ . Předpokládáme přitom, že teplota okolí se přidáním tepla $? Q$ nijak znatelně nezmění. Přivedené teplo je kladné, a proto je také změna entropie kladná. Entropie soustavy tedy při tomto nevratném ději vzrostla.

Tepelně izolovaná soustava.

Uvažujme tepelně izolovanou soustavu dvou těles 1 a 2 s teplotami $T 1$ a $T 2$ .

Tělesa si mohou vyměňovat tepelnou energii, přičemž celková hodnota tepelné energie zůstává stálá. Získá-li těleso 2 o teplotě $T 2$ teplo $? Q 2$ , musí těleso 1 stejně velké teplo odevzdat, tzn. $? Q 2 = - ? Q 1$ . Bude tedy platit $? Q 1 + ? Q 2 = 0$ .

Změna entropie bude

$mathrm{d}S = mathrm{d}S_1+mathrm{d}S_2 = frac{delta Q_1}{T_1} + frac{delta Q_2}{T_2} = left(frac{1}{T_1}-frac{1}{T_2} ight) delta Q_1 = frac{T_2-T_1}{T_1T_2} delta Q_1$

Z tohoto vztahu je vidět, že pokud mají výraz $T 2 - T 1$ a teplo $? Q 1$ stejné znaménko, pak $d S > 0$ , jinak $d S < 0$ . Podle Clausiovy formulace druhé hlavní věty však teplo nemůže samovolně přecházet z tělesa chladnějšího na těleso teplejší. Je-li tedy $T 2 > T 1$ , nemůže teplo přejít z tělesa 1 na těleso 2, a proto musí být $? Q 1 > 0$ , tzn. $? Q 2 < 0$ . Pokud však $T 2 < T 1$ , nemůže teplo přejít z tělesa 2 na těleso 1, takže musí být $? Q 1 < 0$ , tedy $? Q 2 > 0$ . V obou případech mají $T 2 - T 1$ a $? Q 1$ stejná znaménka, což znamená, že v izolované soustavě platí

d S > 0

Celková entropie izolované soustavy dvou těles různých teplot tedy roste. Jsou-li teploty dosti blízké, nebo jsou-li tělesa od sebe dostatečně dobře izolována, může být změna entropie libovolně malá. V takové soustavě prakticky nedochází k výměně tepla a soustava je blízká tepelné rovnováze. Děje, které probíhají v takové soustavě lze považovat za vratné, a jejich entropie se téměř nemění. Při vratném adiabatickém ději může být tedy entropie stálá, avšak nikdy nemůže klesat.

V tepelně izolované soustavě probíhají děje adiabatické. V každé soustavě mohou z počátečního stavu vzniknout různé stavy vratnou nebo nevratnou změnou. Stavy, kterých soustava dosáhne nevratnou změnou se podle druhé termodynamické věty liší od stavů při vratné změně tím, že z nich soustava sama od sebe bez vnějšího zásahu nemůže přejít zpět do výchozího stavu. Mimoto jsou zde stavy, z nichž lze počátečního stavu soustavy dosáhnout nevratnou změnou. Tyto stavy však soustava nemůže z počátečního stavu dosáhnout bez vnějšího zásahu. Odsud plyne další možné vyjádření druhé hlavní věty termodynamiky: V blízkosti každého stavu soustavy existují stavy, kterých nelze dosáhnout adiabatickým dějem. Takové stavy jsou tedy v izolované soustavě vyloučeny.

Podle Carnotovy věty je účinnost nevratného kruhového děje mezi teplotami $T 1$ a $T 2$ vždy nižší než účinnost vratného Carnotova cyklu mezi stejnými teplotami. Pokud tedy pracovní látka získá při nevratném ději teplo $Q 1$ a odvede teplo $Q_2^prime$ , bude platit

$frac{Q_2^prime}{Q_1} > frac{T_2}{T_1}$

Vydané teplo $Q_2^prime$ je vlastně záporné přijaté teplo, tzn. $Q_2^prime = -Q_2$ , tzn.

$frac{Q_1}{T_1} + frac{Q_2}{T_2}<0$

Pokud děj neprobíhá pouze mezi dvěma teplotami, ale při spojitě se měnících teplotách, přejde předchozí součet v limitě na integrál po uzavřené cestě

$oint_{(nevrat)} frac{delta Q}{T} < 0$

Tento vztah se obvykle zapisuje ve tvaru

$oint frac{delta Q}{T}le 0$ ,

kde znaménko rovnosti platí pro vratný kruhový děj. Jde vlastně o vyjádření skutečnosti, že při libovolném kruhovém ději, při němž se teplo mění v mechanickou energii, nemohou být všechna $? Q$ , která soustava přijímá, kladná, ale některá musí být také záporná. Část tepla tedy musí soustava odvádět, takže se všechno přijaté teplo nezužitkuje pro mechanickou energii. Pokud při nevratném ději působí tření, takže vykonaná práce je menší a v soustavě vzniká třením teplo, je třeba k dosažení výchozího stavu odvádět více tepla než při vratném kruhovém ději, což je vyjádřeno znaménkem nerovnosti.

Pokud se entropie procesu zvyšuje, je tento proces nevratný (ireverzibilní). Pokud zůstává konstantní, je tento proces vratný (reverzibilní), jako např. u ideálního Carnotova kruhového děje.

Celková entropie uzavřeného systému se nemůže nikdy zmenšit. V přírodě tedy všechny děje směřují do více neuspořádaného stavu. Stejně tak roste entropie ve vesmíru. Dle předpokladů L. Boltzmana se jeví jako nejpravděpodobnější konečný stav vyrovnání pohybových energií molekul. To znamená, že by se konečné hodnoty entropie ve vesmíru dosáhlo tehdy, kdyby se vyrovnaly veškeré teplotní rozdíly (tepelná smrt).

Informační entropie

Informační entropie velmi úzce souvisí s termodynamickou entropií, ačkoliv toto spojení se ukázalo být zřejmé až po mnoha letech nezávislého studia termodynamické entropie a informační entropie. Často je také nazývana Shannonovou entropií po Claude E. Shannonovi, který zformuloval mnoho klíčových poznatků teoretické informatiky. Obecně pro systém s konečným počtem možných stavů $Sin{s_1,s_2,...,s_n}, nleq infty$ a pravděpodobnostní distribucí $P (s i)$ je informační entropie definována jako střední hodnota:

$H(S)=-sum_{i=1}^n P(s_i)log_{2}P(s_i)$

Zde formálně definujeme, že $0cdot log_{2}0equiv 0$ .

Entropie je maximální pro rovnoměrné rozložení $P(s_i)=frac{1}{n} mbox{ pro } forall{i}$ :

$H(S)=-sum_{i=1}^n frac{1}{n}log_{2}frac{1}{n}=-log_{2}frac{1}{n}=log_{2}n$ ,

a minimální pro zcela deterministický systém $exists P(s_k)=1mbox{ a }P(s_i)=0 mbox{ pro } forall{i} eq k$ :

$H(S)=-sum_{i=1}^n P(s_i)log_{2}P(s_i)=-log_{2}1 = 0$ .

Stručně řečeno, entropie je střední hodnota informace jednoho kódovaného znaku. Entropie souvisí s problematikou generování náhodných (resp. pseudonáhodných) čísel, sekvence naprosto náhodných čísel by měla mít maximální míru entropie. Shannonova entropie také tvoří limit při bezeztrátové kompresi dat, laicky řečeno, komprimovaná data nelze beze ztráty informace „zhustit“ více, než dovoluje jejich entropie.

Podrobnější informace naleznete v článcích , en:Information entropy, de:Entropie (Informationstheorie) a pl:Entropia (teoria informacji).

Vytisknout referát Přidat referát do záložek

Na-mobil.cz

Spřátelené weby

Překlady levně a kvalitně
Účetnictví
Společenské hry - společenské deskové hry
Tvorba www stránek - Webové stránky, SEO
Puzzle-prodej.cz - puzzle na prodej Ravensburger
Puzzle
Seminární práce
SMS zdarma
Na-mobil.cz
Dějepis.info
Referáty-seminárky.sk

Přidat stránku k oblíbeným

Nejnovější v diskusi

Diskusní fórum »

TIP: Chcete zkrátit dlouho chvíli sobě nebo blízkému?
Klikněte na Puzzle-prodej.cz a vyberte si z 5000 motivů skladem!

TIP: Hračky a hry za dobré ceny?
Klikněte na Hračky obchod.cz a vyberte si z tisícovky hraček skladem!