Bipartitní graf
Kategorie: Nezařazeno (celkem: 23181 referátů a seminárek)
Informace o referátu:
- Přidal/a: anonymous
- Datum přidání: 12. srpna 2008
- Zobrazeno: 1966×
- Licence: GNU Free Documentation License
- Seznam autorů a změn
- Vyloučení odpovědnosti
Příbuzná témata
Bipartitní graf
Pojmem bipartitní graf se v teorii grafů označuje takový graf, jehož množinu vrcholů je možné rozdělit na dvě disjunktní množiny tak, že žádné dva vrcholy ze stejné množiny nejsou spojeny hranou.
Definice
Graf G = (V,E) je bipartitní, pokud platí 
a 
. Platí-li navíc 
(tedy v grafu existují všechny hrany s touto vlastností), nazývá se tento graf úplný bipartitní. Značí se Km,n, kde m a n jsou velikosti obou partit.
Vlastnosti
- obě partity grafu jsou podle definice nezávislé množiny a graf přímo implikuje jedno možné 2-obarvení
- platí i obrácené tvrzení - všechny 2-barevné grafy jsou bipartitní
- jednoduchým algoritmem lze v lineárním čase zjistit, zda je daný graf bipartitní a také nalézt jeho 2-obarvení (průchodem do hloubky)
- každý strom je bipartitní
- graf je bipartitní právě tehdy, neobsahuje-li kružnici liché délky
K-partitní graf
Pojem bipartitnosti lze zobecnit na libovolné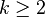 
. Je-li G = (V, E) graf a V lze rozložit na k disjunktních podmnožin takových, že žádné dva vrcholy ze stejné podmnožiny nejsou spojeny hranou, pak tento graf nazýváme k-partitním grafem. Je-li tento graf úplný (ve stejném smyslu jako úplný bipartitní graf, viz výše) a počty vrcholu v jednotlivých partitách jsou 
, pak se tento graf značí 
a nazývá se úplný k-partitní graf.