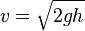Bernoulliho rovnice

Kategorie: Nezařazeno (celkem: 23181 referátů a seminárek)

Informace o referátu:

Příbuzná témata

Vytisknout referátPřidat referát do záložek

Bernoulliho rovnice

Tento článek pojednává o mechanice tekutin. O diferenciální rovnici pojednává článek Bernoulliova rovnice.

Bernoulliho rovnice je vztah užívaný v mechanice tekutin, který odvodil Daniel Bernoulli a který vyjadřuje zákon zachování mechanické energie pro ustálené proudění ideální kapaliny. (Energie je v rovnici přepočtena na objemovou jednotku kapaliny.)

frac{1}{2} ho v^2 + p + ho u(mathbf{x}) = mathrm{konst.}

kde ? je hustota kapaliny, v je rychlost proudění, p je tlak v kapalině a u je gravitační potenciál v daném bodě. První člen v Bernoulliho rovnici představuje kinetickou energii, druhý člen představuje tlakovou potenciální energii objemové jednotky kapaliny a třetí člen (gravitační) potenciál, ve kterém se kapalina nachází. Součet kinetické energie a potenciální energie (tlakové + gravitační) je ve všech místech trubice stejný. Tato rovnice bývá často uváděna ve tvaru, který platí pro homogenní gravitační pole

frac{1}{2} ho v^2 + p + ho g h = mathrm{konst.}

Platí, že pokud na kapalinu v klidu působí tíhová síla, je ve stejné hloubce v každém bodě stejný tlak. Pokud je kapalina v pohybu tak tento vztah neplatí. Slovy můžeme Bernoulliho jev popsat takto: v místě s větším průřezem má proudící kapalina větší tlak, ale menší rychlost, zatímco v místě s menším obsahem průřezu má menší tlak, ale větší rychlost. (Fakt, že při větším průřezu je rychlost kapaliny menší je důsledkem rovnice kontinuity.)

Odvození pro nestlačitelnou kapalinu

Diagram k odvození Bernoulliho rovnice
Diagram k odvození Bernoulliho rovnice

Pokud kapalina o jednotkové hmotnosti m proudí ve vodorovné trubici o průřezu S rychlostí v, platí pro ni pohybová rovnice:

mathrm{d}m frac{mathrm{d}v}{mathrm{d}t} = -mathrm{d}F.

Rozepíšeme tuto rovnici tak, aby v ní vystupovala hustota a průřez trubice

ho S ,mathrm{d}x ,frac{mathrm{d}v}{mathrm{d}t} = -S,frac{mathrm{d}F}{S}=-S,mathrm{d}p.

S využitím vztahu

frac{mathrm{d}v}{mathrm{d}t} = frac{mathrm{d}v}{mathrm{d}x},frac{mathrm{d}x}{mathrm{d}t} = frac{mathrm{d}v}{mathrm{d}x},v=frac{mathrm{d}}{mathrm{d}x}left(frac{v^2}{2} ight)

tato rovnice přejde na

ho S ,mathrm{d}x ,frac{mathrm{d}}{mathrm{d}x}left(frac{v^2}{2} ight) = -S,mathrm{d}p,

tedy

ho ,frac{mathrm{d}}{mathrm{d}x}left(frac{v^2}{2}+p ho^{-1} ight) = 0,

což zintegrováním dá

ho frac{v^2}{2}+ p = mathrm{konst.}

Pokud se navíc nacházíme v potenciálu nějaké síly (např. gravitace), přičteme tento potenciál ?u k tlakovému potenciálu, čímž přímočaře získáme rovnici

ho frac{v^2}{2}+ p + ho u(mathbf{x}) = mathrm{konst.}


Poněkud přímější odvození vychází ze zákona zachování energie. U kapalin uvažujeme potenciální energii tlakovou Ep = pV.

Za předpokladu, že Ek + Ep + Eg = konst., potom platí

1/2 m v2 + p V + m g h= konst.,

vztažením energie na jeden kilogram tekutiny (vydělením hmotností) dostaneme tzv. energetický tvar rovnice:

frac12 v^2 + {pVover m} + g h = mathrm{konst.}

nebo tlakový tvar:

frac12 ho v^2 + p + ho g h= mathrm{konst.}

případně výškový tvar:

{v^2over 2g} + {pover ho g} + h= mathrm{konst.}


Důsledky

Z Bernoulliho rovnice vyplývá, že tlak proudící kapaliny klesá s rostoucí rychlostí. Pokud plyn proudí trubicí dostatečnou rychlostí, tlak v tom místě se natolik zmenší, že toho lze využít například pro odsávání. Tomuto jevu se říká hydrodynamický paradox (hydrodynamické paradoxon) a využívá se ho například u rozprašovačů, natěračských pistolí nebo v karburátoru.

Výtoková rychlost

Ze zákona zachování energie lze také odvodit vztah pro výtokou rychlost kapaliny při vytékání z nádoby s hladinou ve výšce h. Neboť lze říci, že výtoková rychlost kapaliny je stejná jako rychlost, kterou by kapalina získala při volném pádu z výšky h:

v = sqrt{2gh}

Související články

Vytisknout referátPřidat referát do záložek

Nový příspěvek


Ochrana proti spamu. Kolik je 2x4?


Na-mobil.cz

Spřátelené weby

Přidat stránku k oblíbeným

Nejnovější v diskusi

Diskusní fórum »

TIP: Chcete zkrátit dlouho chvíli sobě nebo blízkému?
Klikněte na Puzzle-prodej.cz a vyberte si z 5000 motivů skladem!
TIP: Hračky a hry za dobré ceny?
Klikněte na Hračky obchod.cz a vyberte si z tisícovky hraček skladem!