Banachův prostor

Kategorie: Nezařazeno (celkem: 23181 referátů a seminárek)

Informace o referátu:

Příbuzná témata

Vytisknout referátPřidat referát do záložek

Banachův prostor

Banachovy prostory jsou normované lineární prostory, které jsou navíc úplné. Jsou to jedny z ústředních objektů zkoumání funkcionální analýzy. Jsou pojmenovány podle Stefana Banacha, který je studoval.

Definice

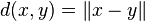Banachovým prostorem rozumíme úplný normovaný lineární prostor. To znamená, že Banachův prostor je vektorový prostor V nad tělesem reálných nebo komplexních čísel s normou |.|, ve kterém má každá cauchyovská posloupnost v indukované metrice d(x,y) = |x - y| limitu.

Příklady

  • Prostory mathbb{R}^n a mathbb{C}^n (všechny n-tice reálných či komplexních čísel) jsou Banachovy v libovolné normě. Opatříme-li prostory mathbb{R}^n a mathbb{C}^n eukleidovskou normou
|x| := sqrt{|x_1|^2+cdots+|x_n|^2},
pro x = (x_1, ldots ,x_n), budou dokonce Hilbertovy.
|f|_infty := max_{t in [a,b]} |f(t)|
je Banachův.
  • Vybavíme-li předchozí prostor normou
|f|_1 :=int_a^b |f(t)|dt nebo |f|_2 :=sqrt{int_a^b |f(t)|^2dt},
Banachův již nebude.
  • Jestliže X je normovaný lineární prostor a Y je Banachův prostor, potom prostor všech omezených lineárních operátorů z X do Y s normou
|A| := sup{|Ax|: xin X, |x|leq 1}
je Banachův prostor. Speciálně duální prostor X* k prostoru X je vždy Banachův, neboť v takovém případě Y=mathbb{C}.

Související články

Vytisknout referátPřidat referát do záložek

Nový příspěvek


Ochrana proti spamu. Kolik je 2x4?


Na-mobil.cz

Spřátelené weby

Přidat stránku k oblíbeným

Nejnovější v diskusi

Diskusní fórum »

TIP: Chcete zkrátit dlouho chvíli sobě nebo blízkému?
Klikněte na Puzzle-prodej.cz a vyberte si z 5000 motivů skladem!
TIP: Hračky a hry za dobré ceny?
Klikněte na Hračky obchod.cz a vyberte si z tisícovky hraček skladem!