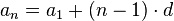Rychlá navigace: obsah, klávesové zkratky, navigace, vyhledávání.

Vložit nový referát | Diskusní fórum

Aritmetická posloupnost

Kategorie: Nezařazeno (celkem: 23181 referátů a seminárek)

Informace o referátu:

Přidal/a: anonymous
Datum přidání: 11. srpna 2008
Zobrazeno: 6894×
Licence: GNU Free Documentation License
Seznam autorů a změn
Vyloučení odpovědnosti

Příbuzná témata

Vytisknout referát Přidat referát do záložek

Aritmetická posloupnost

Aritmetická posloupnost je druh matematické posloupnosti. Hodnota n-tého členu je rovna součtu d a předešlého členu, kde d (rozdíl dvou po sobě jdoucích členů) se nazývá diference aritmetické posloupnosti, přičemž se předpokládá $d e 0$ .

Vzorce

V následujících vzorcích označuje $a n$ n-tý člen aritmetické posloupnosti a d její diferenci. V některých případech jsou uvedeny dva tvary vzorců - pro případ, že prvním členem posloupnosti je $a 0$ resp. $a 1$ . Pokud je uveden vzorec jediný, platí v obou případech.

Rekurentní zadání

$, a_n = a_{n-1} + d$

nebo

$, a_{n+1} = a_n + d$

Zadání vzorcem pro n-tý člen

$a_n = a_0 + ncdot d$

nebo

$a_n = a_1 + (n - 1)cdot d$

Vyjádření s-tého členu z r-tého

$a_s = a_r + (s-r)cdot d$

Součet prvních n členů

$s_n = frac{(a_0 + a_n)cdot (n+1)}{2}$

nebo

$s_n = frac{n cdot (a_1 + a_n)}{2} = n a_1 + frac{1}{2}n (n-1)d$

Odvození vzorce pro součet prvních n členů

Předchozí vzorec lze odvodit následujícím způsobem.

Součet prvních $n$ členů poslouposti lze spočítat „hrubou silou“ následovně:

$s_n = a_1 + a_2 + ldots + a_n$ ,

Vezměme v úvahu nejprve součty sudého počtu prvních n členů, tedy $n = 2 k$ :

Uvažujme dvojice tohoto typu (první a poslední člen, druhý a předposlední, atd.) jako součty :

$a_1 + a_{2k} = a_1 + a_1 +(2k-1)d = 2a_1 + (2k-1) cdot d$ ,

$a_2 + a_{2k-1} = a_1 + d + a_1 + (2k-2) cdot d = 2a_1 + (2k-1) cdot d$ ,

…

$a_k + a_{2k-(k-1)} = a_1 + (k-1) cdot d + a_1 +(2k-(k-1)-1)) cdot d = 2a_1 + (2k-1) cdot d$ ,

Všimněme si, že takovýchto dvojic je právě $k$ a jejich jednotlivé součty jsou stále stejné, tedy celkový součet můžeme vyjádřit takto: libovolná z těchto dvojic (vezměme tu první) krát $k$ (počet takovýchto dvojic).

$s_n = k cdot (a_1 + a_{2k}) = frac {n cdot (a_1 + a_n)}{2}$

Pro liché $n$ bude úvaha obdobná, položme $n = 2 k + 1$ :

$a_1 + a_{2k+1} = a_1 + a_1 +(2k)d = 2a_1 + (2k) cdot d$ ,

$a_2 + a_{2k} = a_1 + d + a_1 + (2k-1) cdot d = 2a_1 + (2k) cdot d$ ,

…

$a_k + a_{2k-(k-2)} = a_1 + (k-1) cdot d + a_1 +(2k-(k-2)-1)) cdot d = 2a_1 + (2k) cdot d$ .

Tedy opět vycházejí u $k$ takovýchto dvojic stejné součty, ale nesmíme zapomenout na $k + 1$ člen, který nemá podle tohoto schématu jiný člen do dvojice, sečtěme ve dvojici $a k + 1 + a k + 1$ :

$a_{k+1} + a_{k+1} = a_1 + k cdot d + a_1 + k cdot d = 2a_1 + (2k) cdot d$ .

Opět vyšel stejný součet jako u předchozích dvojic. Do celkového součtu tedy musíme zahrnout $k + frac {1}{2}$ dvojic:

$s_n = (k + frac {1}{2}) cdot (a_1 + a_{2k+1})$

Po dosazení za $k$ ze vztahu $n = 2 k + 1$ dostáváme stejný vzorec jako pro součet sudého počtu členů:

$s_n = frac {n cdot (a_1 + a_n)}{2}$

tudíž tento vzorec platí pro libovolný počet prvních $n$ členů.

Tento vzorec odvodil ve svých devíti letech (v roce 1786) německý matematik Carl Friedrich Gauss.

Příklad

Například je-li $a 0 = - 5$ a $d = 3$ , pak několik prvních členů aritmetické posloupnosti je: -5, -2, 1, 4, 7, 10, 13, …

Aritmetická řada

Součet členů aritmetické posloupnosti je označován jako arimetická řada.

Součet aritmetické řady je dán jako limita posloupnosti n-tých částečných součtů. Platí tedy

$lim_{n o infty} s_n = pm infty$ ,

kde kladné znaménko platí pro $d > 0$ a záporné pro $d < 0$ .

Aritmetická řada je tedy divergentní.

Související články

Související články obsahuje
Portál Matematika

Geometrická posloupnost

Vytisknout referát Přidat referát do záložek

Na-mobil.cz

Spřátelené weby

Překlady levně a kvalitně
Účetnictví
Společenské hry - společenské deskové hry
Tvorba www stránek - Webové stránky, SEO
Puzzle-prodej.cz - puzzle na prodej Ravensburger
Puzzle
Seminární práce
SMS zdarma
Na-mobil.cz
Dějepis.info
Referáty-seminárky.sk

Přidat stránku k oblíbeným

Nejnovější v diskusi

Diskusní fórum »

TIP: Chcete zkrátit dlouho chvíli sobě nebo blízkému?
Klikněte na Puzzle-prodej.cz a vyberte si z 5000 motivů skladem!

TIP: Hračky a hry za dobré ceny?
Klikněte na Hračky obchod.cz a vyberte si z tisícovky hraček skladem!